SKALA DAN PROYEKSI
Skala
Skala Peta merupakan komponen peta yang sangat penting karena dengan skalapeta kita dapat mengetahui jarak antara dua tempat.
Skala Peta adalah perbandingan antara jarak di peta dengan jarak sebenarnyadipermukaan bumi.
Contoh:
Pada peta tertulis skala 1 : 1.000.000 ini berarti tiap jarak 1 bagian di peta samadengan jarak 1.000.000 bagian di muka bumi.
Jadi kalau di peta itu 1 bagian = 1 cm maka di muka bumi = 10 Km.
Ukuran jarak yang digunakan dalam peta yaitu cm, m, km, inci dan mil. UntukIndonesia satuan yang umum dipakai cm, m, atau km.
BENTUK ATAU MACAM SKALA PETA
Setiap peta hendaknya mencantumkan skalanya agar pembaca dapatmenghitung dan memperkirakan perbesaran pada keadaan yang sebenarnya.
Skala Peta dibedakan menjadi 3 macam, yaitu:
1. Skala Angka/Skala Pecahan (Numerical Scale).
Skala ini sering disebut skala numeric yaitu skala yang dinyatakan dalambentuk perbandingan angka.
Contoh:
Skala 1 : 100.000, skala 1 : 2.000.000 dan sebagainya Bila peta berskala 1 : 100.000 berarti tiap satuan panjang pada peta menggambarkan jarak yang sesungguhnya di lapangan/ di muka bumi sebenarnya 100.000 kali satu satuanpanjang di peta. Bila satuan panjang menggunakan cm berarti tiap jarak 1 cmpada peta menggambarkan jarak
100.000 di lapangan.
Contoh negara yang menggunakan sistem skala angka ini adalah Indonesia danAmerika
Serikat. Untuk menentukan skala peta ini dapat dipakairumus:
2. Skala Verbal yaitu skala yang dinyatakan dengan kalimat atau kata-kata.
Skala ini disebut juga skala inci dibanding mil yang dalam bahasa Inggrisdisebut “Inch Mile Scale”.
Contoh:
Skala dalam suatu peta dinyatakan dalam 1 inch to 5 miles, ini berarti jarak 1 incidi peta menggambarkan jarak 5 mil di lapangan atau jarak sebenarnya.
3. Skala Garis (Line Scale)/Skala Grafik (Graphical Scale) / Skala Batang(Bar Scale)/ Skala Jalan (Road Scale)
Untuk skala ini dinyatakan dalam bentuk garis lurus yang terbagi dalam beberapabagian yang sama panjangnya.
Pada garis tersebut harus dicantumkan ukuran jarak yang sesungguhnya dilapangan, misalnya dalam meter, kilometer, feet atau mil.
Dari grafik tersebut dapat dibaca bahwa tiap jarak 1 inci pada peta samadengan 2 mil di lapangan. Skala garis ini pada umumnya digunakan apabilasuatu peta akan dikecilkan atau akan dibuat ukuran tertentu. Dengan memakai skala grafik/garis maka jarak dua tempat dapat langsung diukur dalam peta.Tidak jarang dalam satu peta dicantumkan skala angka dan juga skala garis.
Sampai disini apakah Anda dapat memahami? Selanjutnya, dalampembahasan skala peta yang harus Anda ingat adalah semakin besarskalanya, akan semakin kecil kenampakkan wilayah yang digambarkan. Sebaliknya semakin kecil skalanya semakin luas areal kenampakkanpermukaan bumi yang yang tergambar dalam peta.Untuk memahami skala termasuk besar atau kecil dapat dicontohkan sebagai berikut:
- Skala 1 : 50.000
|
lebih besardari
|
1 : 100.000
|
- Skala 1 :200.000
|
lebih besardari
|
1 :2.000.000
|
- Skala 1 :250.000
|
lebih kecil dari
|
1 : 50.000
|
MERUBAH SKALA PETA
Perlu Anda pahami juga bahwa jenis skala peta yang ada dapat diubah sesuaidengan keinginan dan kebutuhan. Lalu bagaimana cara merubahnya?Untuk merubah skala peta ada beberapa cara seperti:
1. Mengubah skala angka ke skala grafik
Contoh:
Dalam peta tertulis skala 1 : 300.000, ubahlah ke dalam skala grafikatau garis.
Penyelesaian:
Skala 1 : 300.000 berarti 1 bagian di peta menunjukkan 300.000 bagian di lapangan. Apabila dibuat dalam cm, maka 1 cm di peta = 300.000 cm dilapangan. Bila dibuat skala grafiknya berarti tiap-tiap cm atau dalam satu kotaknilainya 300.000 cm atau 3 km.
Bila digambarkan skala grafiknya sebagaiberikut:
2. Mengubah skala garis menjadi skala angka
Contoh:
Skala garis digambarkan seperti di bawah ini, ubahlah menjadi skala angka!
Penyelesaian:
Pada peta dengan skala ini berarti tiap panjang garis (kotak) menggambarkan 2 km di lapangan sehingga apabila tiap kotak antara 0 –. 2 – 4 dan 4 – 6 masing-masing jika diukur = 2 cm maka:
2 cm = 2 km
1 cm = 1 km
1 cm = 100.000 cm
Sehingga skala angkanya menjadi 1 :100.000
3. Mengubah skala angka menjadi skala inci - mil
Contoh:
Skala angka 1 : 500.000, ubahlah menjadi skala inci-mil
4. Mengubah skala grafik menjadi skala mil-inci
Contoh:
Jika diketahui grafik sepanjang 5 cm menunjukkan jarak 10 mil di lapangan,ubahlah menjadi skala angka dan inci-mil
5. Mengubah skala dengan sistem grid bujur sangkar (Gridsquare)
Sistem grid bujur sangkar disebut juga metode Union Jack
Contoh:
Peta dengan skala 1 : 200.000 ubahlah menjadi peta berskala 1 : 100.000
Bila digambarkan bentuk petanya sebagai berikut:
CARA MENENTUKAN SKALA PETA
Dalam kehidupan sehari-hari sering kita menjumpai peta yang tidak ada skalanya,padahal mungkin kita membutuhkannya. Apabila Anda mengalami kejadian ini makacara menentukan skala peta dengan langkah-langkah sebagai berikut:
1. Membandingkan dua jarak tempat di peta dengan jarak kedua tempat dilapangan
Contoh:
Jarak antara Jakarta dan Bekasi di lapangan 20 km (2.000.000 cm). Di peta jarakkeduanya
50 cm. Tentukan skala petanya!
- Ukur jarak 2 tempat yang diketahui dalam kedua peta itu.
Peta I = jarak A – B = 20 cm
Peta II = jarak A – B = 4 cm
- Pada peta I jarak A – B dilapangan:
= 2 x 50.000 cm = 100.000 cm
- Pada peta I jarak AB
|
=
|
20x
|
x cm
|
=
|
20x cm
|
20x
|
=
|
200.000 cm
|
x
|
=
|
10.000 cm
|
Jadi skala peta I = 1 : 10.000
Dari penyelesaian contoh soal tersebut dapat dibuat kesimpulan rumusan sebagaiberikut:
1. Membandingkan kenampakan-kenampakan dalam peta yangsudah pasti ukurannya.
Contoh:
Dalam peta terdapat lapangan sepak bola panjang lapangan 100 meter = 10.000 cm. Jadi skala lapangan sepak bola tersebut 1 : 10.000
2. Menentukan dua titik di peta yang belum ada skalanya (peta x) misalnyatitik A – B
dengan arah Utara - Selatan.
Setelah itu menghitung jarak dua titik dan selisih derajat garis lintangnya. PerluAnda ingat bahwa jarak tiap 10 garis lintang = 111 km dan 10 = 60 detik
Contoh:
Jarak A - B di peta x = 50 cm Selisih garis lintangnya = 30 detik Berapa skala peta x?
1. Pada peta Topografi (peta Kontur) di Indonesia berlaku rumus:
CI (Contour Interval ) adalah selisih ketinggian antara dua garis kontur yangdinyatakan dalam meter. Contour Interval sering disebut jarak antara garis kontur.Garis Kontur yaitu garis-garis pada peta yang menghubungkan titik-titik yangmemiliki ketinggian yang sama dari permukaan air laut.
Perhitungan CI misalnya:
Pada peta kontur Indonesia yang berskala 1 : 100.000, berapakah CInya?
Apabila Anda ingin mengukur jarak pada peta baik lurus atau berbelok-belok,lakukanlah hal-hal berikut:
a. Gunakan seutas benang yang agak besar (misal: benang kasur)
b. Berilah tanda pada peta di bagian yang diukur.
c. Ukurlah dengan benang yang sudah dipersiapkan.
d. Tekuklah benang mengikuti jarak obyek yang diukur, seperti jalan yangberbelok, benang juga harus ikut dibelokkan.
e. Jarak yang diukur pada peta misalnya 50 cm (antara kota A dengan kota B).
f. Sesuaikan dengan skala garis misalnya skala yang ada 1 : 50.000, maka jarakantara kota A dan B dilapangan = 50 cm x 50.000 = 2.500.000 cm = 25 km.
BENTUK GEODESI BENTUK BUMI
Geodesi merupakan salah satu cabang ilmu matematika untuk pengukuranbentuk dan ukuran bumi, menentukan posisi (koordinat) titik-titik panjang, arah-arahgaris di permukaan bumi, juga mempelajari gravitasi bumi.
GEOID BUMI
Bidang ekuipotensial bumi yang dianggap berhimpit dengan permukaan air laut rata rata. Untuk mengetahui bidang geoid diperlukan pengukuran gaya berat. Saat ini digunakan beberapa pendekatan model geoid secara global diantaranya EGM 96, EGM 2008 , dll. Namun di Indonesia model global tersebut masih memilki ketelitian yang cukup rendah ( kurang lebih 1 meter ), karena masih relative sedikit lokasi pengukuran gaya berat di Indonesia. Geoid disebut sebagai model bumi yang mendekati sesungguhnya. Lebih jauh geoid dapat didefinisikan sebagai bidang ekipotensial yang berimpit dengan permukaan laut pada saat keadaan tenang dan tanpa gangguan , karena itu secara praktis geoid dianggap berhimpit dengan permukaan laut rata-rata (Mean sea level-MSL). Jarak geoid terhadap ellipsoid disebut Undulasi geoid (N). Nilai dari undulasi geoid tidak sama di semua tempat, hal ini disebabkan ketidakseragaman sebaran densitas massa bumi. Untuk keperluan aplikasi geodesi, geofisika dan oseanografi dibutuhkan geoid dengan ketelitian yang cukup tinggi.
BENTUK BUMI
Datum geodesi, proyeksi peta, dan system-sistem referensi koordinat yang telah dikembangkan sejak dulu digunakan untukmendeskripsikan bentuk permukaan bumi beserta posisi dan lokasi geografi dariunsure-unsur permukaan bumi yang menarik bagi manusia.
Bentuk bumi yang telah dianut oleh manusia telah berevolusi dari abadkeabad, antara lain:
a) Tiram atau cakram yang terapung di permukaan laut, menurut bangsa Babilonpada 2500 tahun SM
b) Lempeng dasar, bangsa Yunani kuno pada 500 SM
c) Kotak persegi panjang, geograf Yunani kuno pada 400 SM
d) Piringan lingkaran atau cakram (bangsa Romawi)
e) Bola - bangsa Yunani kuno: Phytagoras (495 SM), aristothelesmembuktikannya (340 SM), Archimides (250 SM), dan Erastosthenes (250 SM)
f) Buah jeruk asam (J. Cassini 1683-1718)
g) Buah jeruk manis – Huygens (1629-1695), dan Issac Newton (1643 – 1727)
h) Ellips putas- French academy of science (1666)
Salah satu tugas geodesi geometris adalah menentukan koordinat titik-titik,jarak, dan arah di permukaan bumi untuk keperluan praktis maupun ilmiah. Untuk itu diperlukan adanya bidang hitungan. Permukaan bumi merupakan permukaansangat tidak teratur. Oleh karena itu, permukaan ini tidak dapat digunakan sebagaibidang hitungan geodesi.
Untuk kebutuhan perhitungan geodesi, permukaan bumi diganti dengan permukaan yang teratur dengan bentuk dan ukuran yang mendekati bumi. Permukaan yang dipilih adalah bidang permukaan yang mendekati bentukdan ukuran geoid. Geoid memiliki bentuk yang sangat mendekati ellips putar dengan sumbu pendek sebagai sumbu putar yang berimpit dengan sumbu putar bumi. Ellipsoid digunakan sebagai bidang hitungan geodesi, yang kemudian disebut sebagai ellipsoid referensi. Ellipsoid referensi biasanyadidefinisikan oleh nilai-nilai jari-jari equator (a) dan pegepengan (b) elipsputarnya. Sedangkan parameter seperti setengah sumbu pendek( c), eksentrisitas (d), dan lainnya dihitung dengan menggunakan ke dua nilaiparameter pertama diatas. Tiap Negara memiliki pandangan berbeda ttg parameter- parameter ini. Indonesia pada 1860 menggunakan ellips Bessel1841 dengan a=6,377,397; dan 1/f = 299.15. tetapi sejak 1971 menggunakan Ellips GRS-67 dengan a=6,378,160;
1/f=298.247.
DATUM GEODESI
Untuk pekerjaan geodesi, selain ellipsoid referensi, diperlukan juga suatudatum yang mendefinisikan system koordinat. Datum secara umum merupakanbesaran-besaran atau konstanta yang dapat bertindak sebagai referensi atau dasar untuk hitungan besaran yang lain. Datum geodesi merupakan sekumpulan konstanta yang digunakan untuk mendefinisikan system koordinat yang digunakan untuk control geodesi. Untuk mendefinisikan datum geodesi yanglengkap diperlukan 8 besaran:
(a) tiga konstanta (X0, Y0, Z0) untuk mendefinisikan titik awal sistemkoordinat, (b) tiga besaran untuk menentukan arah sistem koordinat,dan
(c) dua besaran lainnya ( setengah sumbu a, dan pegepengan f) untukmendefinisikan ellpsoid.
Gambar Datum Geodesi
Datum Lokal
Datum lokal adalah datum geodesi yang menggunakan ellipsoid referensiyang dipilih sedekat mungkin dengan bentuk geoid lokal (tidak luas) yangdipetakan - datumnya menggunakan ellipsoid lokal. Indonesia (1862-1880) telah melakukan penentuan posisi di pulau jawa dengan metode triangulasi.Penentuan posisi ini menggunakan ellipsoid Bessel 1841, sebagai ellipsoid referensi, meridian Jakarta sebagai meridian nol, dan titik awal (lintang) beserta sudut azimutnya diambil dari triangulasi di puncak gunung Genoek (dikenal sbg datum Gonoek).
Tahun 1970-an, untuk keperluan pemetaan rupa bumi pulau Sumatera,BAKOSURTANAL menggunakan datum baru, datum Indonesia 1974 (Padang), yang menggunakan ellipsoid GRS-67 (a= 6,378,160.00; 1/f = 298.247), dikenalsebagai SNI (Speroid National Indonesia). Untuk menentukan orientasi SNI di dalam ruang, ditetapkan suatu datum relatif dengan eksentris (stasiun Doppler)BP-A (1884) di Padang sebagai titik datum SNI.
Pada tahun 1996 ditetapkan penggunaan datum baru, DGN-95, untukseluruh kegiatan survey dan pemetaan di wilayah RI yang dituangkan dalam SKBakosurtanal HK.02.04/II/KA/96. DGN-95 memiliki parameter ellipsiod a=6.378.137,00 dan 1/f=298,257223563.
Datum Regional
Datum regional adalah datum geodesi yang menggunakan ellipsoid referensi yang dipilih sedekat mungkin dengan bentuk geoid untuk area yangrelatif luas (regional) – datumnya menggunakan ellipsoid regional. Datum inidigunakan bersama oleh beberapa negara yang berdekatan dalam satu benuayang sama. Contoh datum regional:
· Amerika Utara 1983 (NAD83) digunakan bersama oleh negara-negarayang terletak di benua Amerika bagian utara
· European datum 1989 (ED89) yang digunakan oleh negara-negara yang terletak di benua eropa,
· Australian Geodetic Datum 1998 (AAGD98) yang digunakanbersama oleh negara-negara yang terletak dibenua Australia
Datum Global
Datum global adalah datum geodesi yang menggunakan ellipsoid referensi yang dipilih sedekat mungkin dengan bentuk geoid untuk seluruh permukaan bumi – datumnya menggunakan ellipsoid global. Contohnya, 1984 departemen pertahanan amerika (DoD) mempublikasikan datum WGS84. Datumini dikembangkan oleh DMA (Defense Mapping Agency) merepresentasikanpemodelan bumi dari standpoint gravitasional, geodetik, dan geometrik denganmenggunakan data teknik, dan teknologi yang sudah ada.
Catatan:
(a) sumbu Z : mengarah ke kutub utara CTP (Convensional terrestrial pole)sebagaimana telah didefinisikan oleh BIH (Bureau International deL’Heure)
(b) Sumbu X: merupakan garis berpotongan antara bidang meridianreferensi WGS 84 dengan bidang ekuator CTP (convensional TerrestrialSystem).
(c) Sumbu Y: sumbu X yang diputar 90o ke arah timur di bidang equator CTP
Demikian pentingnya datum global WGS’84 ini hingga GPS-punmenggunakannya sebagai datum untuk menentukan posisi-posisi tiga dimensidari target-target yang ditentukan.
Transformasi Datum
Pada gambar dibawah ini menunjukkan bahwa permukaan local ellipsoid(yang digunakan oleh datum local) mendekati bentuk geoid hanya di daerah survey yang relative sempit. Jika ellipsoid ini diperbesar sehingga bentuk permukaannya mendekati geoid yang lebih luas, mencakup beberapa Negara,bahkan satu benua, disebut datum regional. Sedangkan jika ellipsiodnyamendekati bentuk geoid secara keseluruhan permukaan bumi, maka ellipsoidnya disebut sebagai datum global.
Gambar Datum lokal dan global
Untuk keperluan survey geodesi yang lebih luas, seperti penentuan batas-batas antara negara- negara yang bersebelahan, maka diperlukan datumbersama. Jika negara-negara ybs masing- masing menggunakan datum lokal yang berbeda, maka masing-masing harus ditransformasikan ke datum yangsama.
Prinsip transformasi datum adalah pengamatan pada titik-titik yang sama.Selanjutnya, titik- titik sekutu ini memiliki koordinat-koordinat dalam berbagaidatum. Dari koordinat-koordinat ini dapat diketahui hubungan matematis antaradatum-datum ybs. Hubungan matematis antara datum ini dapat dinyatakandengan 7 parameter transformasi sbb: Translasi titik asal (origin) dx, dy, dz; rotasisumbu koordinat rx, ry, rz, dan skala S.
Datum Horizontal
Ellipsoid referensi yang paling sering digunakan sebagai bidang untukpenentuan posisi horizontal (lintang dan bujur), yang datumnya dikenal sebagaidatum horizontal. Koordinat posisi horizontal ini beserta tingginya di ataspermukaan ellipsoid dapat dikonversikan ke sistem koordinat kartesian 3D yangmengacu pada sumbu-sumbu ellipsoid ybs.
Datum vertikal
Untuk mempresentasikan informasi ketinggian atau kedalaman, seringdigunakan datum yang berbeda. Pada peta laut umumnya dgunakan suatu bidangpermukaan air rendah (chart datum) sebagai bidang referensi, sehingga nilai-nilaikedalaman yang direpresentasikan oleh peta laut ini mengacu pada pasut rendah(low tide).
SISTEM REFERENSI GEODESI
Agar hasil pengamatan di bidang geodesi dapat saling dibandingkan,dikaitkan, digunakan, atau mendukung hasil-hasil pengamatan di bidang ataudisiplin ilmu lainnya (astronomi, geofisika), maka dibuatlah suatu sistemreferensi geodesi (Geidetic Reference System - GRS).
PROYEKSI PETA
a. Konsep proyeksi peta
Teknik proyeksi ini juga berlaku untuk memindahkan letak titik-titik pada permukaanbumi ke bidang datar yag dinamakan PROYEKSI PETA.
Secara khusus pengertian dari proyeksi peta adalah cara memindahkan sistemparalel (garis lintang) dan meridian (garis bujur) berbentuk bola (Globe) ke bidang datar (peta). Hasil pemindahan dari globe ke bidang datar ini akan menjadi peta.Pemindahan dari globe ke bidang datar harus diusahakan akurat. Agarkesalahan diperkecil sampai tidak ada kesalahan maka proses pemindahan harusmemperhatikan syarat-syarat di bawah ini:
1. Bentuk-bentuk di permukaan bumi tidak mengalami perubahan(harus tetap), persis seperti pada gambar peta di globe bumi.
2. Luas permukaan yang diubah harus tetap.
3. Jarak antara satu titik dengan titik lain di atas permukaan bumi yangdiubah harus tetap.
Di dalam proses pembuatan peta untuk dapat memenuhi ketiga syarat di atas sekaligus adalah suatu hal yang tidak mungkin. Bahkan untuk dapat memenuhi satusyarat saja untuk seluruh bola dunia juga merupakan hal yang tidak mungkin, yang bisa dipenuhi hanyalah satu saja dari syarat-syarat di atas dan ini hanya untuksebagian kecil dari muka bumi.
Secara sederhana dapat dikatakan bahwa dalam membuat peta kita hanyadapat menggambar beberapa bagian permukaan bumi. Untuk dapat membuatpeta yang meliputi wilayah yang lebih luas atau bahkan seluruh permukaan bumi. Untuk dapat membuat peta yang meliputi wilayah yang lebih luas atau bahkan seluruh permukaan bumi kita harus mengadakan kompromi antara ketiga syarat diatas. Sebagian dampak kompromi tersebut, keluarlah bermacam-macam jenisproyeksi peta. Masing-masing proyeksi mempunyai kelebihan dan kelemahansesuai dengan tujuan peta dan bagian mukabumi yang digambarkan.
Bila diminta untuk memetakan seluruh permukaan bumi, maka Anda dituntutharus tepat dalam memilih proyeksi yang digunakan. Pemilihan proyeksitergantung pada:
· Bentuk, luas dan letak daerah yang dipetakan.
· Ciri-ciri tertentu atau ciri asli yang akan dipertahankan.
Sekarang perhatikan terlebih dahulu gambar berikut ini!
Pada gambar 03.3 anda dapat melihat perubahan bentuk dari segi empat pada globe:
Sebagai akibatnya dapat dilihat pada gambar 03.4 berikut ini
Pada gambar 03.4 bagian tengah globe yaitu daerah sekitar garis khatulistiwasedikit mengalami distorsi (penyimpangan) sedangkan daerah kutub mengalamidistorsi yaitu menjadi lebih besar.
Proyeksi ini cocok untuk mempertahankan bentuk sekitar khatulistiwa.
Titik singgung antara permukaan bola bumi dan bidang datar dapat terletak pada kutub, ekuator atau antara kutub dan ekuator.
Misalnya Anda akan memproyeksikan garis-garis meridian dan garis-garis lintang.Jika titik singgung antara bidang datar dan permukaan bola bumi terletak di kutub utara, setelah diproyeksikan garis lintang akan taampak sebagai lingkaran konsentris yang mengelilingi kutub. Garis meridian akan tampak sebagai garis lurusyang berpusat di kutub dengan sudut yang sama.
Perhatikan gambar berikut
Pada gambar 03.6 Anda dapat melihat perubahan bentuk pada garis lingkaranterluar. Garis tersebut lebih besar dari garis di globe. Jadi paling banyak mengalamidistorsi. Pada bagian kutub relatif tidak mengalami perubahan atau distorsi, jadi hampir mendekati kesesuaian. Proyeksi ini cocok untuk mempertahankan bentuksekitar kutub.
Macam-macam proyeksi peta
1. Berdasarkan sifat asli yangdipertahankan
a. Proyeksi Ekuivalen adalah luas daerah dipertahankan sama, artinya luasdi atas peta sama dengan luas di atas muka bumi setelah dikalikan skala.
b. Proyeksi Konform artinya bentuk-bentuk atau sudut-sudut pada petadipertahankan sama dengan bentuk aslinya.
c. Proyeksi Ekuidistan artinya jarak-jarak di peta sama dengan jarak di mukabumi setelah dikalikan skala.
2. Berdasarkan Kedudukan SumbuSimetris
a. Proyeksi Normal, apabila sumbu simetrisnya berhimpit dengan sumbu bumi.
b. Proyeksi Miring, apabila sumbu simetrinya membentuk sudut terhadapsumbu bumi. c. Proyeksi Transversal, apabila sumbu simetrinya tegak luruspada sumbu bumi atau
terletak di bidang ekuator. Proyeksi ini disebut juga Proyeksi ekuatorial.
3. Berdasarkan bidang asal proyeksi yangdigunakan
a. Proyeksi Zenithal (Azimuthal), adalah proyeksi yang menggunakanbidang datar sebagai bidang proyeksinya. Proyeksi ini menyinggung bolabumi dan berpusat pada satu titik.
Untuk memperjelas silahkan perhatikan lagi gambar 03.5.
Proyeksi ini menggambarkan daerah kutub dengan menempatkan titikkutub pada titik pusat proyeksi.
Ciri-ciri Proyeksi Azimuthal:
a. Garis-garis bujur sebagai garis lurus yang berpusat pada kutub.
b. Garis lintang digambarkan dalam bentuk lingkaran yang konsentrismengelilingi kutub.
c. Sudut antara garis bujur yang satu dengan lainnya pada peta besarnyasama.
d. Seluruh permukaan bumi jika digambarkan dengan proyeksi ini akan berbentuklingkaran.
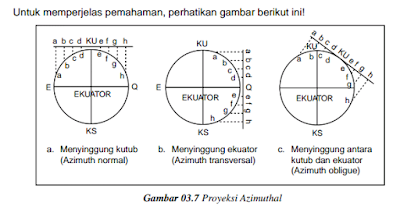
Proyeksi Azimuthal dibedakan 3 macam, yaitu:
a. Proyeksi Azimut Normal yaitu bidang proyeksinya menyinggung kutub.
b. Proyeksi Azimut Transversal yaitu bidang proyeksinya tegak lurus denganekuator.
c. Proyeksi Azimut Oblique yaitu bidang proyeksinya menyinggung salah satu tempat
antara kutub dan ekuator.
Pada gambar 03.6 Anda dapat melihat perubahan bentuk pada garis lingkaranterluar. Garis tersebut lebih besar dari garis di globe. Jadi paling banyak mengalamidistorsi. Pada bagian kutub relatif tidak mengalami perubahan atau distorsi, jadi hampir mendekati kesesuaian. Proyeksi ini cocok untuk mempertahankan bentuksekitar kutub.
Macam-macam proyeksi peta
1. Berdasarkan sifat asli yangdipertahankan
a. Proyeksi Ekuivalen adalah luas daerah dipertahankan sama, artinya luasdi atas peta sama dengan luas di atas muka bumi setelah dikalikan skala.
b. Proyeksi Konform artinya bentuk-bentuk atau sudut-sudut pada petadipertahankan sama dengan bentuk aslinya.
c. Proyeksi Ekuidistan artinya jarak-jarak di peta sama dengan jarak di mukabumi setelah dikalikan skala.
2. Berdasarkan Kedudukan SumbuSimetris
a. Proyeksi Normal, apabila sumbu simetrisnya berhimpit dengan sumbu bumi.
b. Proyeksi Miring, apabila sumbu simetrinya membentuk sudut terhadapsumbu bumi. c. Proyeksi Transversal, apabila sumbu simetrinya tegak luruspada sumbu bumi atau
terletak di bidang ekuator. Proyeksi ini disebut juga Proyeksi ekuatorial.
3. Berdasarkan bidang asal proyeksi yangdigunakan
a. Proyeksi Zenithal (Azimuthal), adalah proyeksi yang menggunakanbidang datar sebagai bidang proyeksinya. Proyeksi ini menyinggung bolabumi dan berpusat pada satu titik.
Untuk memperjelas silahkan perhatikan lagi gambar 03.5.
Proyeksi ini menggambarkan daerah kutub dengan menempatkan titikkutub pada titik pusat proyeksi.
Ciri-ciri Proyeksi Azimuthal:
a. Garis-garis bujur sebagai garis lurus yang berpusat pada kutub.
b. Garis lintang digambarkan dalam bentuk lingkaran yang konsentrismengelilingi kutub.
c. Sudut antara garis bujur yang satu dengan lainnya pada peta besarnyasama.
d. Seluruh permukaan bumi jika digambarkan dengan proyeksi ini akan berbentuklingkaran.
Proyeksi Azimuthal dibedakan 3 macam, yaitu:
a. Proyeksi Azimut Normal yaitu bidang proyeksinya menyinggung kutub.
b. Proyeksi Azimut Transversal yaitu bidang proyeksinya tegak lurus denganekuator.
c. Proyeksi Azimut Oblique yaitu bidang proyeksinya menyinggung salah satu tempat
antara kutub dan ekuator.
Khusus proyeksi Azimut Normal cocok untuk memproyeksi daerah kutub.
Perhatikan gambar berikut ini
Karena proyeksi Azimuthal paling tepat untuk menggambarkan kutub,maka penggambaran kutub melalui proyeksi ini dibedakan menjadi 3macam yaitu:
1. Proyeksi Gnomonik
Pada proyeksi ini pusat proyeksi terapat di titik pusat bola bumi. Ekuatortergambar hingga tak terbatas. Lingkaran paralel berubah ke arah luarmengalami pembesaran yang cepat dan ekuator tidak mampudigambarkan karena pembesaran tak terhingga tadi. Pada daerahlintang 45 akan mengalami pembesaran 3 kali.
1. Proyeksi Azimuthal Stereografik
Titik sumber proyeksi di kutub berlawanan dengan titik singgung bidangproyeksi dengan kutub bola bumi. Jadi jarak antara lingkaran paraleltergambar semakin membesar ke arah luar.
Untuk lebih jelasnya perhatikan gambar berikut ini
1. Proyeksi Azimuthal Orthografik
Proyeksi ini menggunakan titik yang letaknya tak terhingga sebagai titiksumber proyeksi. Akibatnya sinar proyeksinya sejajar dengan sumbubumi.
Lingkaran paralel akan diproyeksikan dengan keliling yang benar atauekuidistan. Jarak antara lingkaran garis lintang akan semakin mengecil bila semakin jauh dari pusat.
. Proyeksi Kerucut (Conical Projection), Proyeksi Kerucut yaitu pemindahangaris- garis meridian dan paralel dari suatu globe ke sebuah kerucut.
Untuk proyeksi normalnya cocok untuk memproyeksikan daerah lintangtengah (miring). Proyeksi ini memiliki paralel melingkar dengan meridianberbentuk jari-jari. Paralel berwujud garis lingkaran sedangkan bujur berupajari-jari.
Perhatikan Gambar berikut ini
Proyeksi kerucut diperoleh dengan memproyeksikan globe pada kerucutyang menyinggung atau memotong globe kemudian di buka, sehinggabentangnya ditentukan oleh sudut puncaknya. Proyeksi ini paling tepat untukmenggambar daerah daerah di lintang 450.
Proyeksi kerucut dibedakan menjadi 3 macam yaitu:
1. Proyeksi kerucut normal ataustandar
Jika garis singgung bidang kerucut pada bola bumi terletak pada suatuparalel (Paralel Standar).
2. Proyeksi Kerucut Transversal
Jika kedudukan sumbu kerucut terhadap sumbu bumi tegak lurus.
3. Proyeksi Kerucut Oblique(Miring)
Jika sumbu kerucut terhadap sumbu bumi terbentuk miring
Dari gambar tersebut dapat dikemukakan ciri-ciri proyeksi kerucutantara lain:
1. Semua garis bujur merupakan garis lurus dan berkonvergensi dikutub.
2. Garis lintang merupakan suatu busur lingkaran yang konsentrisdengan titik pusatnya adalah salah satu kutub bumi.
3. Tidak dapat menggambarkan seluruh permukaan bumi karena salahsatu kutub bumi tidak dapat digambarkan.
4. Seluruh proyeksi tidak merupakan satu lingkaran sempurna, sehinggabaik untuk menggambarkan daerah lintang rendah.
c. Proyeksi Silinder atau Tabung
Proyeksi Silinder adalah suatu proyeksi permukaan bola bumi yangbidang proyeksinya berbentuk silinder dan menyinggung bola bumi.
Apabila pada proyeksi ini bidang silinder menyinggung khatulistiwa, maka semua garis paralel merupakan garis horizontal dan semua garis meridianmerupakan garis lurus vertikal.
Perhatikan gambar-gambar berikut ini
Penggunaan proyeksi silinder mempunyai beberapa keuntunganyaitu:
1. Dapat menggambarkan daerah yang luas.
2. Dapat menggambarkan daerah sekitar khatulistiwa.
3. Daerah kutub yang berupa titik digambarkan seperti garislurus.
4. Makin mendekati kutub, makin luas wilayahnya.
Jadi keuntungan proyeksi ini yaitu cocok untuk menggambarkan daerah ekuator, karena ke arah kutub terjadi pemekaran garis lintang.
Proyeksi Azimuthal,proyeksi kerucut (conical) dan proyeksi silinder(cylindrical) termasuk kelompok proyeksi murni. Penggunaan jenis proyeksi-proyeksi murni ini sangat terbatas.
Nah sampai di sini apakah Anda telah memahami uraian di atas? Bila belumulangi sekali lagi membaca uraian materi di atas dan cobalah menggambarkansetiap jenis proyeksi.
d. Proyeksi Gubahan (Proyeksi Arbitrary)
Proyeksi-proyeksi ini dipergunakan untuk menggambarkan peta-peta yangkita jumpai sehari-hari, merupakan proyeksi atau rangka peta yang diperolehsecara perhitungan.
Contoh-contoh proyeksi gubahan antara lain:
1. Proyeksi Bonne (Equal Area)
Sifat-sifatnya sama luas. Sudut dan jarak benar pada meridian tengahdan pada paralel standar. Semakin jauh dari meridian tengah, bentukmenjadi sangat terganggu. Baik untuk menggambarkan Asia yangletaknya di sekitar khatulistiwa.
1. Proyeksi Sinusoidal
Pada proyeksi ini menghasilkan sudut dan jarak sesuai pada meridian tengah dan daerah khatulistiwa sama luas. Jarak antara meridian sesuai, begitu pula jarak antar paralel. Baik untuk menggambar daerah-daerah yang kecil dimana saja.
Juga untuk daerah-daerah yang luas yang letaknya jauh dari khatulistiwa.Proyeksi ini sering dipakai untuk Amerika Selatan, Australia dan Afrika.
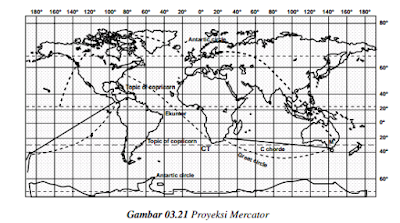
1. Proyeksi Mercator
Proyeksi Mercator merupakan proyeksi silinder normal konform, dimanaseluruh muka bumi dilukiskan pada bidang silinder yang sumbunyaberimpit dengan bola bumi, kemudian silindernya dibuka menjadi bidangdatar.
Sifat-sifat proyeksi Mercataryaitu:
a. Hasil proyeksi adalah baik dan betul untuk daerah dekat ekuator,tetapi distorsi makin membesar bila makin dekat dengan kutub.
b. Interval jarak antara meridian adalah sama dan pada ekuatorpembagian vertikal benar menurut skala.
c. Interval jarak antara paralel tidak sama, makin menjauh dariekuator, interval jarak makin membesar.
d. Proyeksinya adalah konform.
e. Kutub-kutub tidak dapat digambarkan karena terletak di posisitak terhingga.
1. Proyeksi Mollweide
Pada proyeksi ini sama luas untuk berubah dipinggir peta.
Gambar 03.22 Proyeksi Mollweide
1. Proyeksi Gall
Sifatnya sama luas, bentuk sangat berbeda pada lintang-lintang yang mendekati kutub.
DAFTAR PUSTAKA
Amir Syarifudin, Drs. Sri Sudarmi, Dra. Usmaini, Dra, Geografi I, Jakarta: BumiAksara,
2000.
Dinas Pendidikan nasional DKI Jakarta, Program Kerja Guru SekolahMenengah
Umum Kelas I, 1996.
I Made Sandy, Esensi Kartografi.
Sumadi Sutrijat, Geografi I, Departemen Pendidikan Nasional, 1999.
Suyono, dkk, Geografi, Surabaya: SIC, 1995.
TIM Geografi, Geografi I, Jakarta : Yudisthira, 2000.
Wardiyatmoko. K, HR Bintarto, Geografi SMU I, Erlangga, Jakarta: Erlangga, 2000.








































Tidak ada komentar:
Posting Komentar