BAB V RESTORASI DAN KALIBRASI CITRA

 

RESTORASI DAN KALIBRASI CITRA

 

Semua citra digital yang telah terekam oleh sensor dan di simpan dalam format yang dapat di baca program pengolah citra perlu di tampilkan pada layar monitor untuk di analisis dan dan tidakl jarang untuk di cetak. Restorasi citra diperlukan apabila kualitas citra yang di gunakan tidak mencukupi untuk mendukung aplikasi tertentu.namun sebenarnya semua citra yang di peroleh melalui perekaman sensor tak lepas dari kesalahan, yang diakibatkan oleh mekanisme perekaman sensor, gerakan, wujud geometric dan kunfigurasi permukaan bumi, serta kondisi atmosfer pada saat perekaman

Kesalahan yang terjadi pada proses pembentukan citra ini perlu di koreksi supaya aspek geometrid an radiometri yang di kandung oleh citra tersebut benar benar dapat mendukung pemanfaatan untuk aplikasi yang berkaitan dengan pemetaan sumberdaya ddan kajian lingkungan atau kewilayahan lainnya. Beberapa praktisi seringkali menggunakan istilah prapengolahan untuk maksud yang sama karena restorasi vitra memang banyak hal yang perlu diterapkan sebelum dilakukan pengolahan. Khususnya dalam hal ekstrasi informasi

I.                   KUALITAS CITRA

Kualitas citra yang akan di bahas pada sub bab berikut  beberapa dengan pengertian kualitas data spasial secara umum, seperti yang telah di publikasikan secara mendalam oleh Guptill dan Morrison(1995). Kualitas data spasial secara umum yang di maksud oleh Gptill dan Morrison adalah suatu data yang harus di indormasikan kepada para pengguna data agar mereka dapat memanfaatkannya secara prefesional dan juga pada para praktisi atau peneliti yang dalam pekerjaannhya mengahsilkan keluaran berupa peta atau citra agar mencantumkan informasi tentang keadaan data yang dihasilkan sehingga data dapat di manfaatkan sebagaimana mestinya.

Pada bab ini kualitas citra merupakan ukuran kualitatif maupun kuantitatif suatu citra yang akan di proses dengan teknik pengindraan jauh agar dapat menghasilkan informasi tematik spasial turunan yang sesuai dengan standar akurasi yang telah di tetapkan. Secara garis besar, kualitas citra dapat di kelompokan menjadi kualitas geometrid an kualitas radiometri. Geometri dinilai secara kuantitatif berdasarkan tingkat kebenaran (akurasi) bentuk serta posisi objek pada citra, dengan mengacu pada bentuk dan posisi sebenarnya di lapangan ataupun bentuk dan posisi pada peta dengan proyeksi tertentu. Di samping itu, ukuran kualitas geometri terkait erat dengan salah satu aspek kualitas data spasial. Yaitu akurasi posisi

Kualitas radiometri di nilai berdasarkan nyaman tidaknya gambar dalam pandangan secara visual, dan juga benar atau tidaknya informasi spectral yang diberikan objaek dan tercatat pada sensor. Dengan demikian, kualitas radiometri dapat di nilai secara kualitatif dan kuantitatif. Meskipun bersifat kualitatif, nyamannya ganmbar untuk di lihat secara visual sangat berpengaruh pada kemampuan penggunaan citra untuk menurunkan informasi yang ada. Hal ini terutama berlaku bagi analisis atau interpretasi secara visual, bukan berarti bahwa analisis secara digital tidak berpengaruh sama sekali

 

Tinggi rendahnya kualitas citra di pengaruhi oleh banyak hal, antara lain kualitas sensor dan detector, posisi wahana pada saat perekamaan, kondisi daerah yang di liput, dan juga kondisi atmosfer pada saat perekamaan.keadaan awal kualitas citra ini. Apabila sangat rendah, akan berpengaruh secara langsung terhadap kualitas hasil restorasi.perlu juga di tekankan di sini bahwa tinggi rendahnya resolusi(temporal/spectral/spasial)tidak dapat langsung digunakan sebagai ukuran kualitas citra karena aspek resolusi ini tidak lepas dari misi peluncuran wahananya dan tujuan aplikasinya.

 

5.1.1 PENILAIAN KUALITAS CITRA

Penilaian kualitas citra dapat dilakukan secara absolut biasanya mengacu pada beberapa tolak ukur yang jelas, misalnya presentase liputan awan, banyaknya drop out atau kegagalan baris pemindaian, serta korelasi antara saluran pada system multispectral.  Penilaian secara relative biasanya di kaitkan degan potensi citra yang bersangkutan untuk suatu aplikasi tertentu, misalnya survey geologi,kota,ataupun vegetasi.

5.1.2 BEBERAPA PARAMETER KUALITAS CITRA

Berikut ini ulasan singkat tentang beberapa parameter kualitas citra yang digunakan oleh para praktisi, yaitu tutupan awan dan gangguan kabut,korelasi antar salutran,kesalahan geometri, dan kesalahan radiometri.

1 TUTUPAN AWAN DAN GANGGUAN KABUT

Semakin banyak luas liputan awan berarti semakin banyak pula informasi permukaan bumi yang hilang karena tutupan awan dan sekaligus bayangannya. Hal ini sangat berbeda dengan satelit cuaca yang justru banyak membutuhkan informasi mengenai bentuk dan luas liputan awan, demi peramalan gejala gejala atmosfer atau cuaca (Conway dan Maryland Space Consortium 1997) meskipun demikian, sekalipun awan total pada suatu scene hanya 10%, bias jadi liputan tersebut merata pada seluruh wilayah. Hal ini tentu saja menggangu dalam proses interpretasi manual maupun klasifikasi secara digital karena tutupan awan hamper selalu di temani8 oleh tutupan bayangan awan.

Di Indonesia, citra yang 100% bebas awan sangat sulit di peroleh. Hal ini desebabkan oleh waktu perekaman satelit yang bersamaan dengan waktu pembentukan awan dan system sensornya.

System sensor satelit banyak yang di rancang untuk bekerja pada spectra pantulan dan pancaran, baik system multispectral maupun hiperspektral. Dengan demikian, system ini tidak mampu menangkap informasi hamburan balik gelombang mikro yang dapat menembus awan. Pada citra yang di terbitkan oleh berbagai instansi survey pemetaan dan lembaga antariksa, informasi luas liputan awan diberikan salah satu pertimbangan utama.

 

 

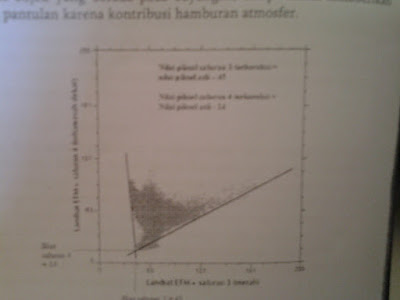
2. KORELASI ANTAR SALURAN

Pada sensor multispectral menghasilkan citra daerah yang sama pada beberapa saluran. Perbedaan informasi spectral objek objek yang sama pada beberapa saluran justru memperkuat kemampuan system dalam membedakan objek satu terhadap yang lain, melalui analisis gugus. Rendahnya hubungan antar saluran menunjukan bahawa satu saluran tidaklah mirip atau tidak hanya menunjukan kecenderungan rona yang terbalik dari saluran yang lain sehingga secara bersama sama saling melengkapi dan dapat di pakai untuk mengenali objek.

Koefisien korelasi merupakan parameter yang sering di gunakan untuk menunjukan kekuatan hubungan antar variable. Dalam citra hal citra multispectral, tiap piksel mempunyai n macam nilai pada n saluran, dan bila seluruh piksel pada 2 saluran diplot pada system 2 dimensi maka nilai koefisien korelasi kedua saluran ini dapat dihitung. Bentuk gugus yang memanjang menunjukan bahwa pola hubungan antara saluran ini cenderung bersifat linier. Bila nilai koefisien korelasinya tinggi, berarti, kedua saluran mempunyai kecenderungan yang sama dalam mempresentasikan objek. Dengan kata lain, keduanya tidak saling melengkapi. Oleh karena itu, semakin tinggi korelasi antar saluran, semakin kedua citra tersebut tidak dapat di andalkan untuk analisis multi spectral.

3. KESALAHAN GEOMETRI CITRA

Citra yang di hasilkan secara klangsung melalui proses perekaman satelit tidaklah bebas dari kesalahan. Kesalahan ini muncul karena adanya gerakan satelit, rotasi bumi, gerakan cermin pada sensor skaner, dan juga kelengkungan bumi. Pada satelit sumber daya yang umumnya mengorbit secara polar atau hampar polar, kombinasi mekanisme lintasan satelitdengan arah rotasi bumi menyebabkan terjadinya pergeseran wujud gambar dari kelompok baris pemindaian ke kelompok baris pemindaian berikutnya. Hasil perekaman juga merupakan model dua dimensi yang menggambarkan kenyataan tiga dimensi pada bidang lengkung permukaan bumi. Disini muncul kesalahan geometri citra yang lain.perbedaan tinggi objek di permukaan bumi secara langsung direkam sehingga menghasilkan citra dengan skala tidak seragam.kesalahan ini di tambah dengan adannya variasi ketinggian lintasan satelit

 

 

4. GANGGUAN DAN KESALAHAN  RADIOMETRI

            Inkonsistensi detector dalam menangkap informasi juga menghasilkan kesalahan berupa anomaly nilai piksel. Piksel ini menjadi bernilai jauh lebih tinggi atau lebih rendah dari yang seharusnya. Keterlambatan dalam memulai baris perekaman baru  juga menghasilkan baris baris perekaman yang cacat. Kesalahan kesalahan tersebut diakibatkan oleh mekanisme internal sensor.

            Gangguan sinyal pada citra dapat berupa kosongnya nilai piksel pada suatu baris pemindaian atau kolom tertentu sehingga piksel piksel tersebut bernilai 0. Gangguan semacam ini dapat pula berupa deretan nilai yang sangat tinggi, kadang kadang 225, berbentuk seperti goresan goresan pada citra secara melintang. Gangguan lain adalah anomaly nilkai piksel secara individual sehingga tidak memepresentasikan informasi spectral yang seharusnya. Gangguan gangguan sinyal semacam ini pada umumnya disebabkan oleh tidak berfungsinya detector pada suatu periode tertentu.

Pada system SPOT, gangguan ini justru terjadi sepanjang kolom, sebagai konsekuensi mekanisme pemindaian push-broom atau along-track scanncing.

Untuk SPOT, upaya mengatasi gangguan-gangguan ini tentunya dilakukan sebelum koreksi geometri awal,mengingat bahwa kolom-kolom yang terganggu akan tergeser posisinya bila pada citra tersebut ditetapkan koreksi giometri awalnya untuk efek kelengkungan dan rotasi bumi, misalnya menggunakan tranformasi indeks vegetasi dan pemfilteran (Danoedoro, 1989).

Informasi dan penyimpanan melalui cara bit-coding, namun sudah tidak lagi mengandung informasi spectral dengan satuan yang lama, melainkan dalam nilai digit 0 – 63, 0 – 127, atau 0 – 255. Semakin banyak energy yang masuk ke sensor, semakin tinggi nilai digit yang dihasilkan.akibatnya informasi pantulan energy yang tercatat sehingga piksel yang bersangkutan akan bernilai 0. Bila kegagalan ini berlangsung dalam selang waktu tertentu maka dihasilkan baris piksel dangan nilai 0 (untuk system perekaman  MSS dan TM Landsat disebut drop-out baris) atau kolom dengan nilai 0 (untuk system perekaman pushbroom SPOT).

Faktor eksternal sensor yang juga memegang peran penting adalah adanya pengaruh atmosfer. Partikel-partikel dalam atmosfer yang kadang-kadang menyerap radiasi pantulan atau pancaran objek, telah mengubah informasi spectral yang mencapai sensor. Beberapa jenis yang dikenal antara lain hamburan Rayleigh, hamburan molekural, hamburan mie.

5.2   KOREKSI (RESTORASI) CITRA

Koreksi citra merupakan suatu operasi pengondisian supaya citra yang akan digunakan benar-benar memberikan informasi yang akurat secara geometris dan radiometris. Operasi koreksi disebut juga perasi pra-pengelolahan (pre-processing). Spectral dan geometris citra seperti seharusnya maka koreksi citra kadang-kadang disebut pula sebagai proses restorasi citra.

5.2.1  KOREKSI GEOMETRI CITRA

Untuk mengatasi kesalahan geometri citra, berbagai macam koreksi dilakukan. Mather (2004) mengelompokan koreksi itu dalam dua kategori besar, yaitu (a) model geometri obiraldan (b) transformasi berdasarkan titik-titik control lapangan (ground control points, GCP). Berikut ini uraian masing-masing metode koreksi secara ringkas.

1.      METODE GEOMETRI ORBITAL

 

Metode koreksi yang mengacu ke model geometri orbital. Banari (1995, dalam Mather, 2004) menjeskan dua prosedur berdasarkan persamaan-persamaan kolinearitas fotogrametri yaitu persamaan karakteristik orbit dan satelit dan geometri arah pandang. Berikut ini factor-faktor yang dikoreksi melalui model geometri orbital ini antara lain :

a.      Koreksi ‘Aspect Ratio’

Untuk mengatasi hal ini maka perlu dipilih apakah piksel dikorekasi menjadi 79 x 79 m atau 56 x 56 m. karena arah pemindaian melintang orbit yang mengalami oversampling maka pemilihan 79 x 79 di pandang lebih rasional. Aspect ratio adalah 56:79 atau 1:1,41. Matriks tranformasi pertama untuk mengoreksi aspect ratio menjadi 1:1 menjadi:

 

 

 

 

b.      Koreksi Kemencengan

Landsat 1-3 mempunyai inklinasi sebesar 99,09°., sementara landsat 4 – 5 dan 7 mempunyai inkliminasi sebesar 98.2°, serta meningkat sejalan dengan bertambah besar lintang, baik utara ataupun selatan. Sudut lintang kemencengan  pada litang tertentu L dalam derajat dinyatakan sebagai :

 

 

 

 

 

 

Pedoman inilah yang dipakai sebagai dasar untuk mengoreksi geometri citra melalui proses rotasi sehingga kenampakan Landsat-7 ETM+ dengan aras (level) koreksi 1G sudah terputar miring ke kanan.

 

c.       Koreksi Rotasi Bumi

Pada saat satelit mengorbit bumi dari arah utara keselatan , satelit juga secara kontinu melakukan perekaman dengan memindai permukaan bumi yang ada dibawahnya. Untuk mengopensasi pasis ini maka diperluakan penentuan parameter berikut: (a) waktu yang di perlukan oleh sensor satelit untuk merekam citra, dan (b) kecepatan sudut rotasi bumi  kearah timur). Baik jarak maupun kecepatan dinyatakan dalam ukuran sudut (angular), misalnya radian, dimana 1 rad kurang lebih sebesar 57°.

 

 

 

Komputasi tersebut dapat diringkas sebagai suku, yang menunjukan besarnya pergeseran posisi karena rotasi bumi dan sekalipun kemencengan (skewness)  orbit satelit dengan rumus sebagai berikut :

 

Mather (2004) Menambahkan bahwa sejumlah piksel ditambahkan pada awal setiap baris pemindaian untuk mengompensasi efek rotasi bumi ini. Jika koreksi ini dipandang cukup maka treansformasi matriks M3 dapat dihilangkan. Namun jika tidak maka penambahan iksel diberikan pada header/trailer  citra yang disosiasikan dengan setiap baris pemindahan, dan pengisian piksel bias dihilangkan sehingga matriks transformasi M3 di terapkan.

Citra yang telah terkoreksi geometri secara sistimatik semacam ini pada umumnya tela siap untuk diproses secara digital untuk ekstraksi informasidan juga untuk interpretasi visual. Kusu pada system MSS landsat, koreksi ini juga meliputi ‘penambahan’ jumlah garis piksel, utuk menyamankan skala sepanjang baris dengan skala sepanjang kolom. Perbedaan skla ini muncul karena system MSS landsat menghasilkan piksel beresolusi 79 (sepanjang kolom) x 54 meter (sepanjang baris).hal ini diakibatkan oleh perbedaan kecepatan gerak putaran cermin dengan kecepatan koding sehingga pada setiap baris, piksel berikutnya sellalu ‘mendidih’ peksel sebeumnya.

Pada system perkaman HRV spot, hal ini tidak terjadi karena tidak adanya mekanisme gerakan cermin. Koreksi hanya dilakukan dengan menghitung magnitude kecepatan rotasi bumi, gerakan satelit, dan sudut pandang sensor. Pada aras (level) ini, citra SPOT-HRV dikatakan memiliki aras koreksi 1-B. koreksi geometri selanjutnya dierlukan untuk menghasilkan data yang lebih teliti dalam aspek planimetrik

2. TRANFORMASI BERDASARKAN GCP

Koreksi geometri menggunakan model geomrti orbital merupakan model fisikal yang mencoba mengenali parameter-parameter penyebab kesalahan secara deduktif, kemudian direkontruksikan. Variasi ketinggian dan sikap/posisi wahana maupun objek tidak ikut diperhiyungkan dalam mdel fisikaal in, semata-mata karena informasi yang diperlukan untuk koreksi ini tidak tersedia (Mather, 2004). Oleh karena itu muncul cara pandang yang berbeda, yang mencoba mengoreksi citra dari sudut pandang empiris, dengan cara membandingkan posisi-posisi yang berbeda dengan citra dan data lapangan/peta yangsdah tersedia .

Piksel yang dimaksud adalah posisi pusat piksel .pada koreksi ini telah dipertimbangkan bahwa perubahan posisi piksel itu juga mencangkup perubahan informasi spektarlnya. Untuk mengatasi hal it, diperlukan interpolasi nili spectral selama tranformasi geometri (yang disebut proses resampling) sehingga dihasilkan geometri baru dengan nilai baru.

a.       Koreksi geometri dengan Rektifikasi Citra ke Peta

Dalam proses ini, system geometri citra diubah menjadi plan metric. Segala aktifitas pemanfaatan citra yang memerlukan koreksi ini. Meskipun demikian metode koreksi ini tidak mampu menghilangkan semua distrosi yang disebabkan oleh pergeseran relief pada citra.

 Proses koreksi ini dimulai dengan memilih pasangan titik-titik kordinat pada citra(baris-klom) dan pada peta(x-y, misalnya pada sitem kodrinat UTM) berdasarkan pasangan titik-titik ini koefisien-koefisien persamaan tranformasi yang digunakan untuk mengubah system kordinat citra ke system koordinat peta akan ditentukan.

 

 

 Cara forward mapping ini tampaknya tidak bermasalah ketika kita mencoba untuk mentranformasi titik-titik krdinat yang bersifat diskret disepanjang kenampakan linier, misalnya jalan atau sungai pada peta fector. Hal ini besa dilakukan dalam pemetaan katografi dan system informasi geografis berbasisi fektor . masalah muncul ketika peta yang dikoreksi adalah peta grid (raster) atau citra digitaldimana diperlukan operasi untuk mengisi grid peta baru (terkoreksi) dengan nilai yang diperoleh dari cita atau citra lama (sebelum koreksi) masalah ini terlihat pada penempatan lokasi baru yang seolah mengembang, tidak tepat pada posisi grid. Utuk mengatasi hal ini , suatu interpolasi nilai diperlukan untuk mengganti nilai lama dengan mempertimbangkan nilai-nilai piksel yang ada disekitarnya. Proses ini disebut dengan proses interpolasi nilai piksel.

 

 

 

Jansen(2005) juga menegaskan secara teroretissemakin tinggi orde polinomnya maka semakin dekat kooesfisie-koefisien tersebut dalam memodelkan kesalahan geometri pada citra asli (sebelum koreksi).

Dalam praktik, persamaan polimonial orde 1 sudah bias dijalankanan pada citra wilayah bermedan yang relative datar, sementara polinom orde yang lebih tinggi untuk citra yang menggambarkan kondidi wilayah yang lebih kasartoopografinya.

Untuk kesalahan-kesalahan yang disebutkan terakir maka polinom orde yang lebih tinggi diutamakan

 

Akurasi Hasil Koreksi Geometri; Rmse

Berdasarkan pasangan koordinat anatara titik control lapanagan (GCP) dengan koordinat baru hasil estimasi, diperoleh selisi pada seanjang sumbu x (arah timur) maupun sumbuh Y (arah utara). Selisih ini dapat dihitug pada setiap titik control dan juga pada hasil transformasi keseluruhan, yang memperhitungkan setiap ttitik control yang ada. Berdasarkan selisih-selisih in kemudian dapat dihitung besarnya akurasi hasil geometri dengan rumus root mean square error (RMSE).

 

Dimana:

N                  = jumlah total titik control lapagan (GCP) yang digunakan dalam koreksi atau rektifikasi

E_i dan N_i       = berturut-turut koordinat x (timur, E) dan Y (utara, N) dari GCP ke-I, yang dihitung        dari fungsi tranformasi f₁ dan f₂yang digunakan dalam rektifikasi.

Ê dan Ň        = koordinat referensi berturut-turut untuk X (timur,E) dan Y(utara,N) yang diperoleh dari pea topografi atau asil pengukuran GPS di lapangan

 

Berdasarkan RMSE_E dan RMSE_N kemudian dapat dihitung nilai indicator akurasi keseluruhan berdasarkan rumus beriku:

 

 

b.      Koreksi geometri dengan rektifikasi citra-ke-citra

Koreksi geometri dengan retifikasi dari citra ke citra merupakan suatu proses yang membandingkan pasangan titik-titik yang dapat diidentifikasi dengan mudah pada kedua citra. Rektifikasi citra ke citra dapat memerlukan hasil yang harus menyajikan informasi tentang koordinat yang benar sesuai dengan peta. Misalnya, dua himpunan data ikonos dab quikbird pada waktu perekaman yang berbeda hendak diperbandingkan kenampakannya, analisi perubahan penggunaan lahan.

 

Interpolasi Intensitas Dalam Koreksi Geometri\

Perhatikan bahwa matriks ata grid dengan posisi koordinat yang bernilai bulat (misalnya x’=3, y’=4; x’=5, y’=2, dan seterusnya) tersebut juga telah ditempati oleh nilai-nilai pikes tertentu pula.

 Alogaritma bilinear interpolation mempertimbangkan ke empat nilai piksel yang berdekatan untuk kemuduan di rata-rata secara proporsional, sesuai dengan jaraknya terhadap posisi baru, dengan mengikuti formula berikut:

Dimana BV_{wt (bilinier)} merupakan nilai piksel baru hasil interpolasi spasial (den koreksi geomeri) yang merupakan rerata tertimbang melalui metode bilinear; Z_k adalah nilai piksel disekitar titik hasil penempatan posisi baru (k=4, karena ada 4 piksel yang ada disekitarnya untuk diprtimbangkan); dan D_k² adalah kuadrat jarak dari titk hasil penentuan lokasi baru yang akan ditentuka nilainya.

 

 

 Bilinear interpolation akan menghasilkan kenampakan yang jauh lebih halus dari pada nearest neighbor, sedangkan cubic convolution justru akan menghasilakn citra dengan kenampakan yang tidak terlalu diperhalus. Alogaritma nearest neighbor lebih sesuai diterapkan pada citra saluran-saluran asli dan juga hasil kasifikasi (yang berupa peta penutup lahan ), namun dengan resiko kenampakan linier yang terpatah-patah (broken)

 Distribusi GCP

Hasil RMSE yang kecil merupakan jaminan bagi bagusnya hasil koreksi geometri secara spasial. RMSE yang sedikit lebih besar kadang-kadang merupakan hasil yang optimal apabila kondisi medan cukup berat dan titik-titik control suli dijumpai

Cara paling bai untuk mengetahui apakah suatu citra telah dikoreksi geometri dengan baik adalah dengan mengeplot peta vector meliputi jaringan jalan, batas-bats penutp lahan, jaringan jalan dan sungai di atas citra terkoreksi. Apabila RMSE cukup kecil dan semua fitur kenampakan topografis terplotkan dengan tepat maka koreksi geometri yang telah dilakkan dapat dipandang cukup baik. Sebaliknya, apabila nilai RMSE relative kecil namun hasil pengeplotan fitur topografis justru meperlihatkan banyaknya penyimpangan posisi  kenampakan hasil koreksi maka sebaiknya proses koreksi geometri perlu diulang, dengan membatalkan dan mengambil kembali titik-titik kontrol   atau GCP.

 

5.2.2 KOREKSI / KALIBRASI RADIOMETRI CITRA

Koreksi radiometri diperlukan atas dua alasan yaitu ubtuk memperbaiki kualitas visual citra dan sekaligus memperbaiki nilai – nilai piksel yang tidak sesuai dengan nilai pantulan atau pancaran spectral objek yang sebenarnya. Koreksi rasiometri citra yang dituunjukan untuk memperbaiki kualitas visual citra berupa pengisisan kembali baris yang kosong karena droop out baris mupun masalah kesalahan awal pemindaian koreksi radiometri yang ditunjukan untuk memperbaiki nilai pikxel supaya sesuai dengan yang seharusnya juga bisa dilakukan dengan memprtimbangkan factor gangguan sebagai sumber kesalahan utama.

I.       Koreksi yang bertumpuh pada informasi dalam citra

a.       PENYESUAIAN HISTOGRAM

Metode ini merupkan pilihan yang paling sederhana dengan hanya melihta histogram setiap saluran secara independen. Dari histogram dapat diketahui nilai piksel terendah saluran tersebut.

 

 

 

b.      PENYESUAIAN REGERESI

Penyesuaian regeresi diterapkan dengan memplot nilai-nilai piksel hasil pengamatan pada beberapa saluran sekaligus. Hal ini  dapat diterapkan apabila saluran rujukan yang menyajikan nilai 0 untuk objek tertentu, misalnya saluran TM7 untuk air jernih, dalam, dan tenang. Kemudian ssetiap saluran di pasangkan dengan saluran rujukan tersebut membentuk diagram pancar nilai-nilai piksel yang diamati

 

 

c.       PENGGUNANAN FUTURE SPACE

Metode ini ditawarkan oleh Bronsveld (1991). Metode ini memanfaatkan gambaran future space hasil pengeplotan piksel-piksel pada saluran hijau melawan infaramerah dekat dengan saluran merah melawan inframerah dekta.pertemuan kedau garais ini diasumsikan harus bertemu di titik asal ( 0,0) yaitu untuk objek air jernih, tenang, dan dalam atau objek bayangan lereng yang sangat curam. Apabila ternyata titk pertemuan ini tidak pada ordinat (0,0) maka nilai offset pada kedua saluran dapat dihitung.

d.      METODE KALIBRASI BAYANGAN

Secara ringkas metode ini mempertimbangkan immbnagan energy elektromagnetik yang msauk ke atmosfer bumui serta kenampakan permukaaan bumi yang tetutup bayangan.

 

 

e.       KALIBRASI RELATIVE ANATRCITRA

Kadang kala suatu penelitian pengindraan jauhmemerlukan data multitemporal bahkan bukan hanya dua atau tiga tanggal melainkan bisa lebih dari itu. Analisis spectral citra memerlukan informasi lengkap mengenai parameter –parameter radiometri sensor dan saat perekaman. Kalibrasi relative merupakan proses pengubahan nilai piksel dari satu atau bebrapa data digital citra, dengan mngacu pada nilai piksel untuk objek yang sama pada citra yang berbeda; baik yang dihasilkan pada waktu yang berbeda, oleh sensor yang berbeda, maupun kombinasi keduanya.

 

f.       KALIBRASI DENGAN DATA DARI LUAR CITRA

Penggunaan metode-metode koreksi atau kalibrasi yang telah dijelaskan pada bagian terdahulu kadang-kadang masih menyisahkan masalah. Misalnya pengkaitan anatra suatu nilai piksel dengan nilai kondisi biofisisk tertentu kadang kala menurut informasi yang lebih akurat pula kebutuhannya bisa lebih dari itu, misalnya hingga informasi tentang beberapa besar energy yang dipantulkan oleh objek di permukaan bumi  sebelum bercampur edngan tambahan informasi spectral dari radiansi ketika data nilai sspektral citra perlu dibandingkan dengan data hasil pengukuran radiansi spectral lapangan.

a.       KALIBRASI BERBASIS DATA EMPIRIS : PENYESUAIAN REGRESI BEBRBASIS DATA SPECTRAL LAPANGAN

Teknik koreksi radiometri dengan menggunakan data empiris hasil pengukurn lapangan juga bisa diterapkan dengan penyesuaiana regeresi. Teknik ini memanfaatkan data spectral hasil pengukuran spektro meter di lapangan untuk objek yang sama pada citra. Hasil pengukuran lapangan dinyatakan dalam pantulan permukaan sementara data citra diubah ke radiansi spektral

 

 

b.      KOREKSI PENGARUH POSISI MATAHARI

Posisi matahari berpengaruh pada respons spectral objek yang tercatata oleh sensor. Dua macam citra wilayaah yang sama namu diperoleh atau direkam dengan posisi matahari yang berbeda akan memberikan informasi spectral yang berbeda ntuk objek yang sama.

untuk mengoreksi posisi matahari ( yang sering juga disebut dengan sun evation angle atau sudut ketinggian matahari) ini digunakan rumus sebagai berikut :

 

 

 

c.       KALIBRASI SENSOR RADIANSI YANG TERCATAT OLEH SENSOR

Seperti yang telah disinggung pada bagian erdahulu nilai piksel yang sama pada citra yang berbeda, misalnya berbeda saluran, sensor, ataupun tanggal perekaman, tidaklah secara lnangsung menggambarkan kekuatatn energy pantulan atau pancaran yang sama yang tercatata oleg sensor. Setiap sensor dan detector dirancang denga kepekaan tersendiri dan ditunjukan oleh kemampuna mendeteksi radiansi spectral minimum maupun maximum dari objek atau target. nilai kepekaan ini dinyatakan sebagai gain dan offset. hubungan antara nilai piksel BV dengan gain dan offset serta radiansi spektralnya dinyatakan sebagai berikut :

 

 

Contoh tersebut berlaku untuk Landsat. Untuk SPOT, perhitungannya menjadi lebih sederhana dalam bentuk :

 

Dimana nilai Gain diperbarui secara regular, mengingat bahwa detector mengalami perubahan kepekaan seiring dengan waktu.

       Pada kasus, header citra yang disertakan dalam pembelian citra kadang-kadang menyertakan nilai radiansi spectral minimum dan maksimum (L_Ϯ(min) dan L_{Ϯ (maks)} agar analisis atau pengguanaan bisa melakukan proses koreksi atau kalibrasi sendiri sesuai dengan rumus yang digunakan. Dalam banyak kasus yang lain, data yang diberikan oleh vendor biasanya menyertakan nilai Gain. Kalau tidak analis citra dan penggunaan bisa mengunjungi situs yang sesuai untuk memperoleh nilai Gain. Masalahnya satuan juga yang diperhatikan agar tidak terdapat kesalahan dalam perhitungan.

     Hal lain yang perlu diperhatikan adalah kenyataan bahwa dalam proses perekaman kadang-kadang citra tersaji dengan kecerahan yang sangat tinggi atau sangat rendah. Untuk mengoreksi citra dengan kecerahan yang sangat rendah, nilai low gain dari operator bisa digunakan, sementara apabila citra terlihat sangat cerah, nilai high gain yang digunakan. Dalam beberapa kasus, nilai gain hanya dinyatakan untuk satu kondisi saja dan kadang-kadang juga untuk banyak kondisi, seperti misalnya ASTER VNIR dan SWIRN.

 

 

 

 

d.  Koreksi Pengaruh Atmosfer

            koreksi berbasis pemodelan efek atmosfer telah dikembangkan oleh beberapa peneliti. Salah satunya adalah model 5s ( simulation of the sensor signal in the solar spectrum ) yang dikembangkan oleh Tanre.et al. (1986,1990) dan kemudian diperbaiki menjadi model 6s (second simulation of the sensor signal in the solar spectrum) (vormote et al. 1997). Model – model ini mampu mensimulasikan permukaan non lambertian untuk memodelkan sinyal yang diukur oleh sensor.

            Dalam model ini ada asumsi bahwa satu paket irradansi matahari utuh datang mencapai bagian teratas atmosfer. Sebagaian dari irradansi yang datang kemudian dihamburkan di sepanjang jalur antara matahari dari objek di permukaan bumi ke atmosfer, sementara sisanya radiasi matahari langsung. Bagian yang diteruskan dan mencapai permukaan objek/target dirumuskan sebagai (Jensen,2005;Tso dan Mather;2009):

 

 

Sementara itu, sebagian dari radiasi matahari yang dihamburkan ke atmosfer juga memberikan sumbangan iliminasi pada target objek di permukaan bumi.

Disamping itu ada juga kontribusi hamburan yang perlu dipertimbangkan yaitu, disebut dengan mekanisme jebakan. Efek mekanisme ini terkait dengan pantulan dan hamburan  radiasi metahari yang berturut – turut target dan atmosfer, yang di antara objek disekitar permukaan target dan atmosfer yang menyebabkan radiasi yang tercatat kemudian merupakan incident upon the graound target.  Dengan demikian iluminasi pada target di permukaan bumi menjadi reflektansi atmosfer ps. dengan demikian, iluminasi pada target di permukaan bumi menjadi:

 

 

  

Karena sensor menerima refleksi dari dua macam sumber, yaitu kontribusi dari radiasi matahsri keseluruhan yang diberikan oleh target di permukaan bumi dan langsung ditransmisikan dari permukaan objek ke sensor, serta sumbangan dari objek di sekitar target yang dihamburkan ke sekitar medan pandang sensor maka rumusnya adalah :

 

Akan tetapi perlu pula diperhatikan bahwa sensor sebenarnya juga menerima sebagian dari radiasi matahari yang telah dihamburkan ke medan padang sensor, tanpa berinteraksi dengan target di permukaan bumi.  Dengan demikian pantulan tereflektansi yang tercatat oleh sensor p adalah :

 

Selanjutnya adanya interaksi atmosfer yang kedua yaitu proses serapan perlu dipertimbangkan. Pada spectrum optic dari matahari, penyerapan atau absorbs oleh gas – gas di atmosfer pada dasarnya terkait dengan keberadaan ozon.  Maka persamaan menjadi :

 

e.  Kalibrasi Sensor: Pantulan yang diterima sensor (At-Sensor Reflectance)

hasil kalibrasi sensor untuk memperoleh nilai radiasi spectral L_Ϯ  (rumus 5,22 dan 5,23) sebenarnya adalah nilai energy yang dicatat oleh sensor (apparent radiance), yang merupakan kombinasi dari pantulan objek ditambah gangguan atmosfer yang sampai ke sensor. Itu sebabnya hasil kalibrasi ini juga sering disebut sebagai at sensor radiance atau at-sensor reflenctance atau at-satelite reflentance.untuk menekan pengaruh gangguan atmosfer maka rumus perhitungan pantulan pada permukiman objek (p = reflectance,atau sering kali disebut at-surface reflectance ) berikut bias digunakan :

f.  Kalibrasi Berbasis Model Transfer Radiasi (Radiative Transfer Model)

kebanyakan model koreksi atau kalibrasi citra dilakukan secara manual- dalam arti perangkat lunak menyediakan semacam image calculator yang secara fleksibel dapat dimanfaatkan untuk berbagai operasi metematis dengan memasukan nama berkas citra atau salah satu/beberapa salurannya, nilai koofisien atau konstanta, serta operator matematis, misalnya fungsi-fungsi trigonometrik dan logaritma melalui cara tersebut, dimasukan berbagai parameter yang diperlukan untuk mengambarkan karakteristik hamburan dan serapan yang terjadi di atmosfer pada tanggal dan waktu tertentu.

 

Algoritma model transfer radiasi untuk koreksi pengaruh atmosfer dapat melakukan hal seperti yang telah dijelaskan sebelumnya dengan lebih baik. Menurut Jensen (2005) syarat yang harus dipenuhi adalah penggunaan memasukan informasi karakteristik fundamental atmosfer ke program, dan terdapat saluran spectral yang peka terhadap serapan serapan atmosfer. Beberapa informasi umum yang diperlukan oleh algoritma koreksi atmosfer berbasis transfer radiasi misalnya :

-          Posisi lintang bujur liputan citra

-          Ketinggian perekaman (ketiangian sensor dan wahana) di atas permukaan medan

-          Elevansi rerataan liputan citra

-          Model, atmosfer misaknya wilayah tropis, lintang sedang di musim panas lintang sedang dimusim dingin

-          Data radiasi spectral citra yang telah dikalibrasi secara radiometri (misalnya data harus diproses dan disajikan dalam satuan W m^-2m sr^-1

-          Informasi tentang setiap saluran secara spesifik

-          Kejernian atmosfer setempat (local atmospheric visibility) pada waktu perekaman

 

Berdasarkan informasi tersebut maka program akan melakukan komputasi karekteristik serapan dan hamburan pada saat perekaman. Data serapan dan hamburan kemudian digunakan untuk melakukan inversi nilai radiansi spectral tiap piksel ke pantulan permukaan yang telah diskalakan (scaled surface reflenctance). Beberapa contoh program pemodelan transfer radiasi misalnya : ,MODTRAN 4+, ACORN, ATREM, FLAASH,  dan ACOR.

 

Beberapa rumus model – model transfer radiasi disajikan menggunakan kode transfer radiasi sebagai berikut :

Ø   ACORN ( atmospheric correction now), program ini menggunakan kode transfer radiasi dari MODTRAN-4 dan dikembangkan oleh Chandrasekhar (1960 dalam Jesen 2005).

Ø   ATREM (atmospheric removal program ) yang di kembangkan oleh center for the study of earth from space (CSES). ATREM mempertimbangkan jimlah hamburan reyleigh yang masih ada dalam model 6s. serta model aerosol yang dispesifikasikan oleh pengguna. Program ini melakukan kalkulasi suku/komponen serapan atmosfer dengan menggunakan model spectral saluran sempit malkumus berdasarkan atmosfer standar yang dipilih oleh pengguna, misalnya temperature, tekanan udara serta distribusi vertikal uap air.

Ø   FLAASH( fat line-of-sight atmospheric analysis of spectral hypercubes) dikembangkan di perangkat lunak ENVI, oleh spectral sciences inc. bekerja sama dengan laboratorium riset angkatan udara. Program FLAASH mengoreksi citra dengan cara menekan atau menghilangkan efek uap air, oksigen, karbon dioksida dll. Koreksi ini diterapkan pada setiap piksel.

Ø   ATCOR, pada walnya program ini dikembangakan di jerman.

 

 

 

 

DAFTAR PUSTAKA

 

Danoedoro,Projo. Penagantar Penginderaan Jauh

Digital .-Ed.1.-Yogyakarta: ANDI.2012